Data Structures
Master the art of organizing and managing data efficiently
About The Subject
Learn the fundamentals of data organization and algorithms
Overview
Data Structures form the foundation of computer science and programming. They define the way data is organized, stored, and accessed efficiently in memory. A well-chosen data structure improves algorithm performance and overall program efficiency, making it a critical part of software development.
Arrays
A collection of elements stored in contiguous memory locations. Useful for storing fixed-size sequential data with constant-time access.
Linked Lists
A dynamic data structure made up of nodes where each node contains data and a pointer to the next node. Allows efficient insertion and deletion.
Stacks
A linear data structure that follows the LIFO (Last In, First Out) principle. Used in function calls, expression evaluation, and backtracking.
Queues
A linear structure that follows the FIFO (First In, First Out) principle. Used in scheduling, buffering, and process management.
Trees
A hierarchical data structure consisting of nodes. Common types include binary trees, BST, AVL trees used in searching and sorting.
Graphs
A collection of nodes (vertices) connected by edges. Used to represent networks like social media, maps, or communication systems.
Faculty Information
Meet your course instructor
Dr. K. M. SUBRAMANIAN
Professor
Syllabus
Complete course curriculum and topics

Study Materials
Download notes and reference materials
Click to download the complete Data Structures notes (PDF, ~4.1MB)
Lab Details
Practical sessions and schedule
Lab Incharge
Dr. K. M. SUBRAMANIAN
Lab Schedule
FRIDAY - 2:00 PM TO 4:30 PM
Lab Location
Data Structures Lab - Block B, 3rd Floor

Important Questions & Answers
Previous year questions with detailed solutions
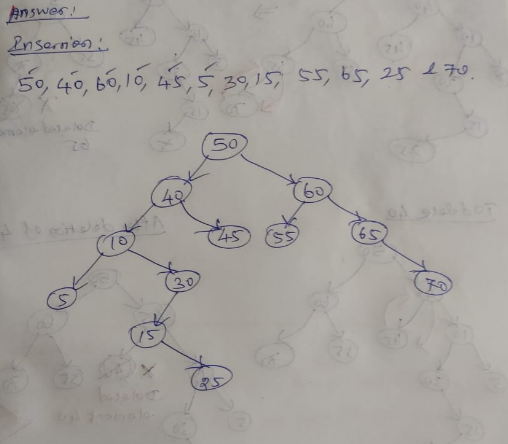
Answer:
SINGLE LINKED LIST:
Single linked list is a sequence of elements in which every element has a link to its next element in the sequence.
OPERATIONS OF SINGLE LINKED LIST:
1. Insertion: Insertion is used to add new node to the list. You can add at any specific position.
Example: Before Inserting 10
26 → 18 → 255 → NULL
After Insertion:
5 → 10 → 26 → 18 → 55 → NULL
2. Deletion: Deletion is used to remove the existing node from the list.
Example: Delete 26
5 → 10 → 18 → 55 → NULL
3. Traversal: Traversal means visiting each node to display or process its data.
Example: Output: 5..10..18..55
4. Searching: Searching is used to find a specific element in the list.
Example: Search for 18 → Found
Answer:
HASH FUNCTION:
- Hashing is the process of mapping large amounts of data item to a smaller table with the help of hashing function
- The value generated by hash function is called "Hash Value" which is used as an index to store values in the Hash Table
DEFINITION:
Hash function is a function which maps key values to array indices OR Hash Function is a function which when applied to the key produces an integer which can be used as an address in a hash table.
EXAMPLE:
Consider that we want to place some employee records in the hash table. The record of an employee is placed with the help of key: employee ID. The employee ID is a 7 digit number for placing the record in the Hash Table. To place the record, 7 digit number is converted into 3 digits by taking only last three digits of the key. If the key is 496700 it can be stored at 0th position. The second key 8421002, the record of those key is placed at 2nd position in the array.
Hence the hash function will be H(key) = key % 1000 where key % 1000 is a hash function and key obtained by hash function is called hash key.
TYPES OF HASH FUNCTION:
There are various types of hash function which are used to place the data in the hash tables:
1. Division Method:
In this method, the hash function is dependent upon the remainder of a division.
Example: Table size is 5, keys are 10, 18, 24, 26 then:
- H(10) = 10 % 5 = 0 → this value is used as an index to store the value in the hash table
- H(18) = 18 % 5 = 3
- H(24) = 24 % 5 = 4
- H(26) = 26 % 5 = 1
2. Mid Square Method:
In this method, firstly key is squared and then mid part of the result is taken as the index.
Example: Consider that if we want to place a record of 3101 and the size of table is 1000. So 3101 × 3101 = 9616201 i.e. h(3101) = 162 (middle 3 digit)
3. Digit Folding Method:
In this method the key is divided into separate parts and by using some simple operations these parts are combined to produce a hash key.
Example: Consider a record of 12465512 then it will be divided into parts i.e. 124, 655, 12. After dividing the parts combine these parts by adding it:
H(key) = 124 + 655 + 12 = 791
4. Multiplication Method:
The given record is multiplied by some constant value. The formula for computing the hash key is:
H(key) = floor(table_size × (key × A) % table_size) where p is integer constant, and A is constant real number
Donald Knuth suggested to use constant A = 0.61803398987
Example: If key = 23 and table_size = 10 then:
H(key) = floor(10 × (23 × 0.61803398987) % 10)
= floor(142.14 % 10)
= 142
At 142 locations in the hash table the record 23 will be placed
Answer:
QUEUES:
- Queue is a linear data structure where the first element is inserted from one end called REAR and deleted from the other end called FRONT
- Front points to the beginning of the queue and Rear points to the end of the queue
- Queue follows the FIFO (First In First Out) structure
- According to its FIFO structure, element inserted first will also be removed first
- In a queue, one end is always used to insert data (enqueue) and the other is used to delete data (dequeue), because queue is open at both its ends
- The enqueue() and dequeue() are two important functions used in a queue

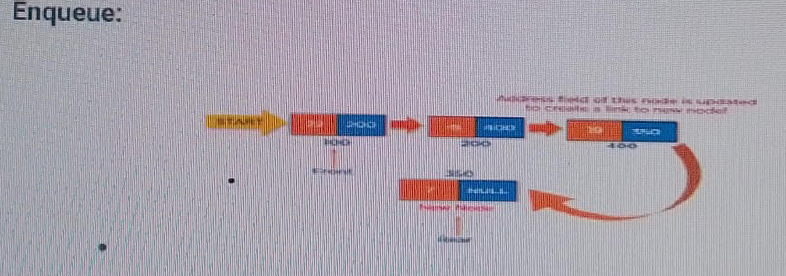
enQueue(value) - Inserting an element into the Queue:
We can use the following steps to insert a new node into the queue:
- STEP 1: Create a newNode with given value and set "newNode→next" to NULL
- STEP 2: Check whether queue is Empty (rear = NULL)
- STEP 3: If it is Empty then, set front = newNode and rear = newNode
- STEP 4: If it is Not Empty then set rear→next = newNode and rear = newNode
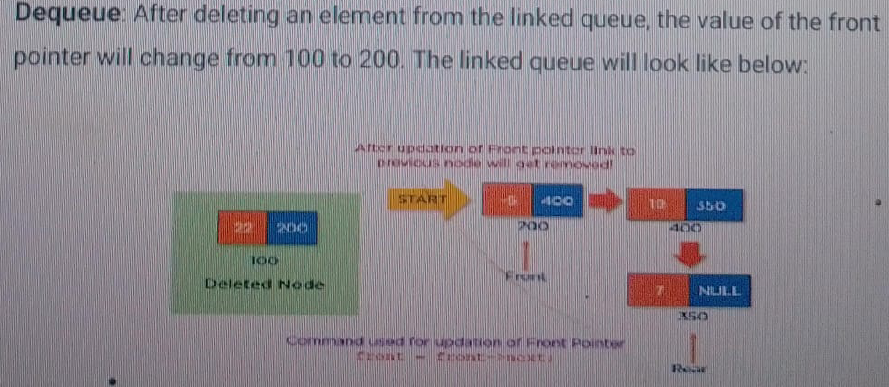
deQueue() - Deleting an Element from Queue:
We can use the following steps to delete a node from the queue:
- STEP 1: Check whether queue is Empty (front == NULL)
- STEP 2: If it is Empty, then display "Queue is Empty!! Deletion is not possible!!!" and terminate from the function
- STEP 3: If it is Not Empty then, define a Node pointer 'temp' and set it to 'front'
- STEP 4: Then set front = front→next and delete 'temp' (free(temp))
display() - Displaying the elements of Queue:
We can use the following steps to display the elements (nodes) of a Queue:
- STEP 1: Check whether queue is Empty (front == NULL)
- STEP 2: If it is Empty then, display 'Queue is Empty!!' and terminate the function
- STEP 3: If it is Not Empty then, define a Node pointer 'temp' and initialize with front
- STEP 4: Display temp→data and move it to the next node. Repeat the same until 'temp' reaches to 'rear' (temp→next != NULL)
- STEP 5: Finally! Display 'temp→data→NULL
Answer:
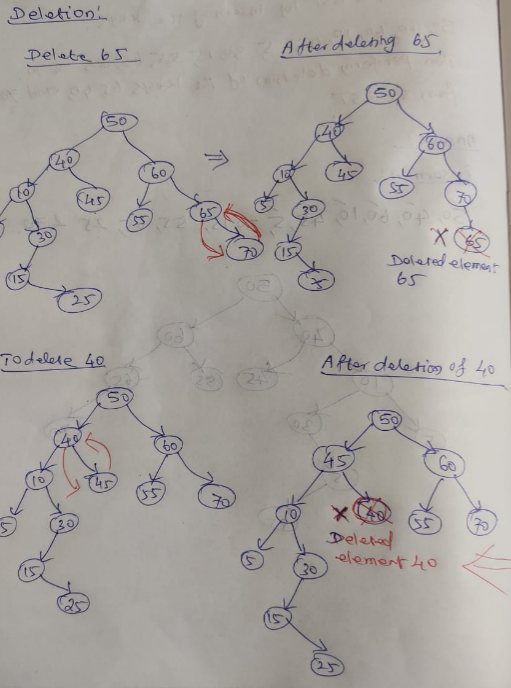
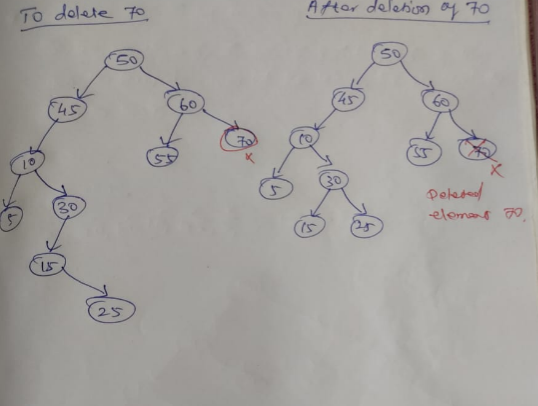
BINARY SEARCH TREE DELETION:
- Delete function is used to delete the specified node from a binary search tree
- First we have to compare the deleted node with root node. If it is less than root node then we have to check left side of the tree. If node to be deleted is greater than parent node we have to check right side of the tree
- There are three situations of deleting a node from a binary search tree
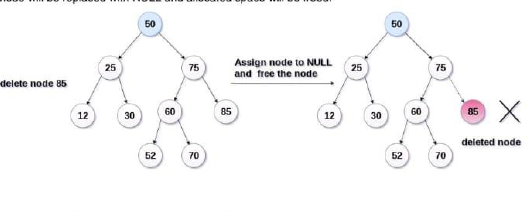
1. Node to be deleted is leaf node:
It is the simplest case. In this case, replace the leaf node with NULL and simply free the allocated space.
In the image we are deleting the node 85. Since the node is a leaf node therefore the node will be replaced with NULL and allocated space will be freed.
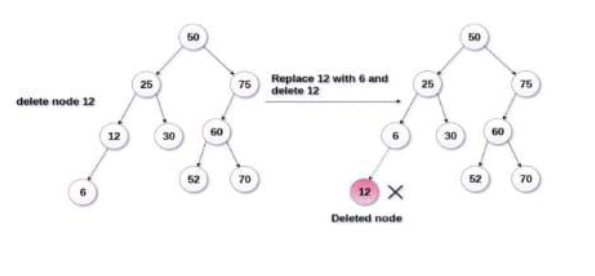
2. The node to be deleted has only one child:
In this case replace the node with its child and delete the child node which now contains the value which is to be deleted. Simply replace it with NULL and free the allocated space.
In the following image the node 12 is to be deleted. It has only one child. The node will be replaced with its child node and the replaced node 12 (which is now leaf node) will simply be deleted.
3. Node to be deleted has two children:
Node which has to be deleted has two children then we can replace that node with:
- a. In order predecessor
- b. In order successor
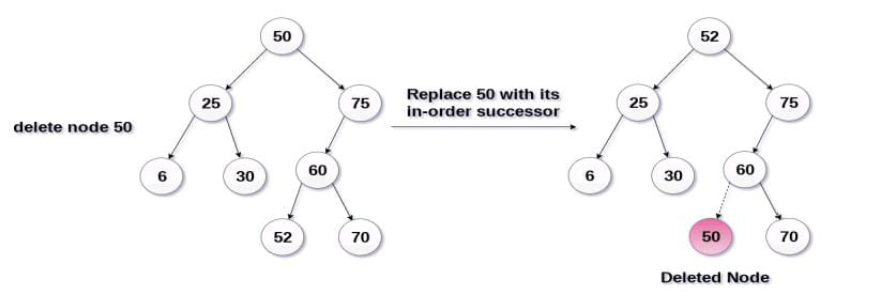
In the following image the node 50 is to be deleted which is the root node of the tree.
The in order traversal of the given tree: 6, 25, 30, 50, 52, 60, 70, 75
Replace 50 with its in order successor 52. Now 50 will be moved to the leaf of the tree which will be simply deleted.
Answer:
SKIP LIST IN DATA STRUCTURE:
- A skip list is a probabilistic data structure. The skip list is used to store a sorted list of elements or data with a linked list. It allows the process of the elements or data to view efficiently. In one single step, it skips several elements of the entire list, which is why it is known as a skip list.
- The skip list is an extended version of the linked list. It allows the user to search, remove, and insert the element very quickly. It consists of a base list that includes a set of elements which maintains the link hierarchy of the subsequent elements.
SKIP LIST STRUCTURE:
It is built in two layers: The lowest layer and Top layer.
The lowest layer of the skip list is a common sorted linked list, and the top layers of the skip list are like an "express line" where the elements are skipped.
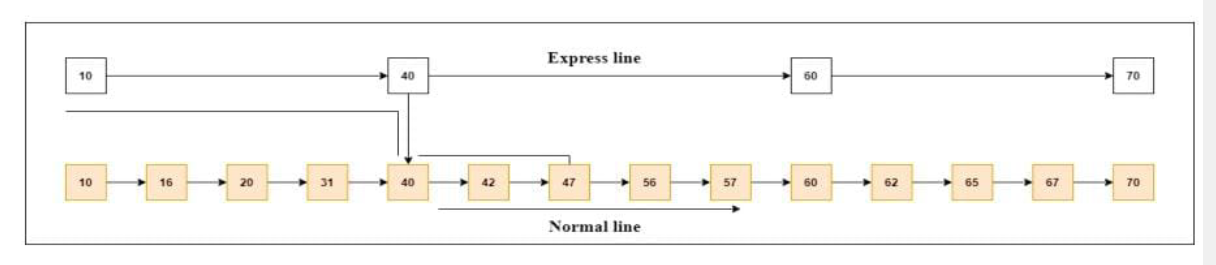
SKIP LIST BASIC OPERATIONS:
These are the following types of operations in the skip list:
- Insertion operation: It is used to add a new node to a particular location in a specific situation
- Deletion operation: It is used to delete a node in a specific situation
- Search Operation: The search operation is used to search a particular node in a skip list
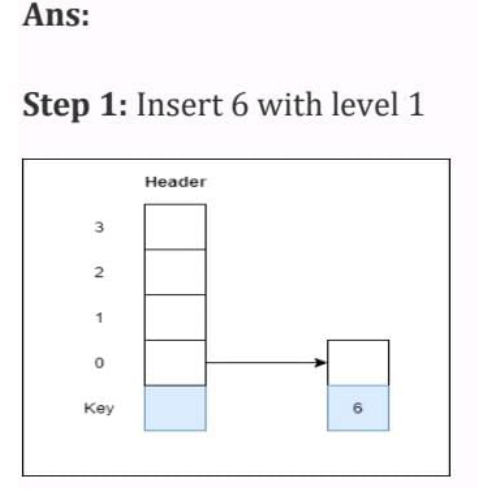
EXAMPLE: Create a skip list, we want to insert these following keys in the empty skip list:
- 6 with level 1
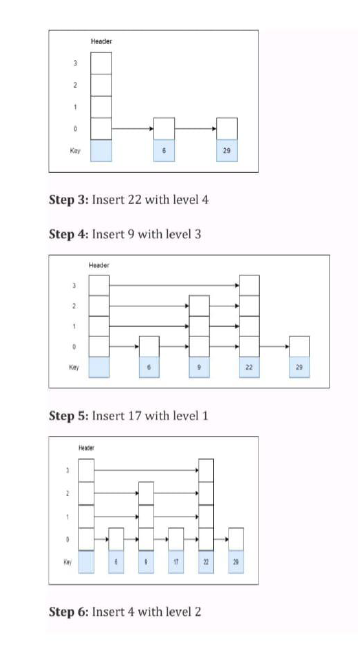
- 29 with level 1
- 22 with level 4
- 9 with level 3
- 17 with level 1
- 4 with level 2
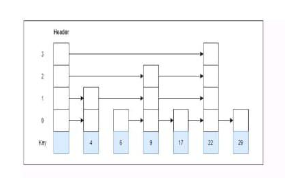
Answer: